ORDINAL REAL NUMBERS 2. The arithmetization of order
types .
By Dr. Constantine E.
Kyritsis
Department of Mathematics
and Computer Science
Software Laboratory
Electrical and Computer Engineering
http://www.softlab.ntua.gr/~kyritsis
§0 Introduction
. In this second paper on ordinal real
numbers are proved, the main (elementary) properties of them. It is proved that
the ordinal real numbers Rá of
characteristic á, is the maximal field of
characteristic á (maximality) and that
it is , according to the theory of
Artin-Screier, a real closed field. (It turned out ,after the work was
completed and by thinking aside, that they are also Archimedean complete (see [ Glayzal A. 1937]),formal power series
fields with real coefficients ,Dedekind complete (see
[Massaza,Carla 1971]), and Pythagorean
fields ).
It is also proved a classification theorem which is
analogous to the Hölder theorem for the Archimedean linearly ordered
fields.In particular it is proved
that any linearly
ordered field of characteristic á contains the field
Qá of ordinal rational numbers
of characteristic á, as a
dense subfield and it is contained in the field Rá of ordinal real numbers of characteristic á, as a subfield ..As it is known, the linear segments
of elementary euclidean geometry can be defined as special order-types with
Archimedean property, and Archimedean (Hilbert) completness through axioms (see
e.g. for a not ancient approach the
Hilbert axiomatisation in [ Hilbert D.1977] ch 1 ).It can be
proved to be
order isomorphic with subsets of the real number field R. This is well-known
and it can be called , the elementary arithmetisation of the order-types of Euclidean linear
segments . On this fact is based the Cartesian idea of analytic geometry. This
was an important turning point in the developments of the ideas and techniques
of mathematics , of the discrete nature
of numbers and continuous nature of geometry. The basic principle is
that the continuum is developed from the
discrete and not vice versa! An instance of this principle is the
development of images and animation in computers through pixels and bits! It is
surprising that in one of the consequences of the theory of ordinal real
numbers, it is proved a far more advanced and complete result for the whole
category of order types that has as corollary the previous important and
elementary arithmetisation. Although more advanced, the result remains in the
context of elementary theory of ordinal real numbers .In this result any order
type can be “discretised” or “arithmetised” through the ordinal numbers.
The process of
definition of the
maximal fields Rá, from the minimal (double well
ordered ) monoids Ná =á, of principal ordinal numbers,we call K-
fundamental densification. It is proved that any order-type is order
isomorphic to a subset of some field Rá. Thus any order-type is constuctible by K-fundamental densification
from ordinal numbers .This is called
the K-arithmetisation of the order-types. Although in
the way it
is presented, this result is
softly obtained, throws new light to the relation of ordinal numbers and
order-types ,this relation turns out to be similar to the elementary relation
of numbers and line segments in
geometry. Also it, holds
a second kind
of arithmetisation ,the
binary arithmetisation which we
state in the same paragraph .
§1
On the topology of linearly ordered fields. Local deepness, á-sequences.
The ordering of any linearly ordered
field F defines a well known topology : the order-topology denoted by T<;
In this topology, as it is known, the field F is a topological field.
This topology has very good separation
properties; it is a T1-T5
topology, that is a completely normal topology (see for instance [ Lynn
A.Steen-Seebach J.A. Jr 1970] § 39 p. 66-68, also see [ Munkress J.R. 1975] Chapters
I, II)
The previously
described order topology is
also called the locally
convex topology compatible with
the order (see [Nachbin L. 1976] Ch I, II).
(The convexity defined by the order).
Definition
1. Let X be a topological space. Let p
X. The least ordinal á such that it exists a (local) base denoted by Bp of open neighbourhoods of the point p
which is an á-sequence such that if x<y<á, Ux Ì Uy, is called local deepness of
X at p.
We notice that the concept of local deepness is very
close to the concept of local weight of
a topological space,
where instead of ordinal we have
an initial ordinal
that is a cardinal number (see [Kuratowski K. 1966]
V-I p. 53-54).
Examples of topological spaces such that every point
has local deepness, are the î*-uniform topological spaces as they are defined in
[Cohen L.W.Goffman C. 1949] pp 66 conditions 1.2.3.4.
As in the case of fields that are
classes, we may
permit topological spaces that are classes and the open sets
is a class of subclasses closed
to union and finite intersection. For
such spaces, the local deepness may be Ù1 that is the
class of all ordinal numbers.
Proposition
2. Let X a topological space
and á, a limit ordinal such that every point has local-deepness
á let AÍX. It holds that 
there
is an â-sequence {xs|s<â} from elements
of A such that 
. In other words topological convergence in X
can be treated
with â-sequences
where â=car(á) is the upper character of á (see
[N.L.Alling 1987] ch 1 §1.30
pp 29)
The proof is almost direct and to save space we shall
not give it here.
Proposition 3. Let a
field denoted by
F of ordinal characteristic á, where á is a limit
ordinal. Then every point xF in the order-topology has
local-deepness car(á),
where car(á) is the
upper character of á (see [ N.L.Alling 1987] ch 1 §1.30 pp 29 ).
The proof is again direct and outside the scope of the
paper.
Corollary
4. Convergence in the order-topology of
a field of ordinal characteristic á, can be treated with â-sequences â³car(á)
Needless to say,
that in the
case in which
the topological space is a class
and the local deepness is Ù1, then
convergence can be treated with Ù1-sequences.
§2 The Holder- type classification .
Lemma 5. In every field of characteristic athe field Qá is a dense
subset.
Proof. Let a field of characteristic á, which we denote
by Fá. By the theorem 17 of
[Kyritsis C. OR1] the field Qá is a
subfield of Fá. Let us suppose that it is not dense in Fá. Then
there are two elements x,y Fá x<y , such that there is no element
of Qá in the internal
[x,y]. Then the
element z =
y-x is Qá-infinitesimal.
This holds because 
where 
similarly. But by the
hypothesis 
and every element of Qá can be written
as r2-r1 where r2 
(y) and r1 
(x). Also
we have that 0<y-x<r2-r1.
Then y-x is a Qá-infinitesimal
and 
is a Qá-infinite element of Fá, thus 
>á, contradiction since Char Fá = á.
Then there are not two element y,x Fá x<y with no element of Qá in [x,y], and Qá is dense in
Fá. Q E D
Remark. Thus every field Fá of characteristic á is a Weil
completion of the field Qá of ordinal
rational numbers (see [ Weil A.]
ChIII Definition 2 but applied not only
to local fields).
Theorem 6 (Maximality or completness
up-to-characteristic ).
The
field Rá is the maximal field,
of characteristic á. In the sense that every field of characteristic á is contained as
subfield of Rá (more
precisely Rá contains an order
preserving monomorphic image of the
field).The field Rá is the unique
fundamentally complete field of characteristic á.
Remark. This theorem is analogous to the well-known
Holders theorem theorem òçéøç óôáôåò that every linearly ordered Archimedean field is a
subfield of the field of real numbers.
In other words the field of real
numbers is the maximal Archimedean linearly ordered field. The previous property of the ordinal
real numbers Rá relative
to their characteristic ,we call maximality or completness up-to characteristic .
But as an erroneous application of
terms R is
also the minimal Cauchy complete
field of characteristic w and this also applies for the fields Rá in the sense that a completion of a linearly ordered
field of characteristic á must be the field Rá .
Proof. Let any field of ordinal characteristic á denoted by Fá. By theorem 17 of [ Kyritsis C. 1991], the field Qá is contained in Fá: QáÍFá. Let x Fá. Let (L(x), R(x)) be the cut that x defines on Qá (L(x) = {v|v Qá v<x}, R(x) = {v|v Qá x<v}). Since Qá is dense in Fá (Lemma 5). There is a Cauchy
á-sequence {xn|n Îw(á)} of
elements of Qá that converges in Fá to x (all
topologies are the order-topologies). Hence QáÍFáÍRá and the field Rá is a maximal field of characteristic á ; but also
the field Rá is actually a minimal Cauchy
complete field of characteristic á in the
sense that the (strong)
Cauchy completion 
of any field Fá of characteristic
á contains the field Rá:QáÍFá has as a
concequence that RáÍ. Thus if Fá is complete then RáÍFá, FáÍRá hence Fá =Rá q.e.d.
The theory of Artin-Schreier of real closed fields has
an excellant application to the ordinal
real numbers .
Corollary
7. The fields of ordinal real
numbers Rá are real closed fields.
Proof.
Direct from Theorem
6 , and remark 5 of [ Kyritsis C.1991] q.e.d.
Post written Remark A. The author
developed the theory of ordinal real numbers during 1990-1992 He had used the
name “transfinite real numbers” without being aware that this term had been
introduced by A.Glayzal during 1937 for his theory of linearly ordered fields.
From the moment he fell upon the work of A.Glayzal (see [ Glayzal A. 1937 ]) in the bibliography of the Book of N.L alling
(see [N.L.Alling 1987 ] ) he changed the title to “Ordinal Real Numbers” .
After the work had been completed ,the
author realised , by thinking aside,
a quite unexpected and not unhappy fact :That the
fields of ordinal real numbers are algebraically and order isomorphic to
the fields of transfinite real numbers
of Galyzal .This can be deduced by the
fact that the fields of transfinite real numbers are exactly all the
Archemidean complete fields (see [Glayzal A. 1937] theorems 4,8,9) and by the
maximality of the ordinal real numbers (theorem 6). Thus if Rá is a field of ordinal real numbers of characterisic
á, any Archemidean
(linearly ordered field ) extension of it ,it shall have the same
characteristic with Rá. It seems
that it can be proved , that any cofinal (coterminal) linearly ordered field extension
,is of
the same characteristic . By the maximality of Rá (theorem 6) it shall have to coinside with Rá. In other words the fields of ordinal real numbers are Archemidean
complete fields (although they may be non-Archemidean ).But this is a characteristic
property of the fields of transfinite real numbersb of Glayzal.
Thus they are order and field isomorphic with fields
of transfinite real numbers .Conversely ,let any field
R(ë) of
transfinite real numbers of
Archemidean base ë. Let us denote
by á its ordinal
characteristic .Let us suppose that there
is an order and field extension of it with the same
characteristic .Then it has to be an Archemidean extension of R(ë). By the Archemidean completness of the transfinite
real numbers ,it has to coinside with the R(ë). Thus the transfinite real numbers are also complete
up-to-characteristic .
But this is a characteristic property of the fields of the ordinal real numbers.Hence they are order and field isomorphic with fields of ordinal real numbers .Thus the ordinal real numbers should be considered as a different technique ,nevertheless indispensable and more far reaching .It is the technique that everyone would like to work.
Post
written Remark B .Let a
field Rá of
ordinal real numbers
of ordinal characteristic á. It is also a field of transfinite
real numbers of archemidean base ë. The set of
all elements of Rá that as formal power series have support of ordinality
less than â£o(ë)=maximum ordinality of well
ordered set of ë, and which we denote
by Rá,â is a field ,subfield of Rá .Indeed Rá,ï(ë) =Rá. For the
applications and especially
with measurment proceeses ,the
fields Rá,ù are of prime interest and
indispensable .
Post
written remark C .The facts of the previous remark ,have as a
concequence that the fields of ordinal real numbers are formal power
series fields with
coefficients in the
real numbers and exponents in some order types.Thus the
n-roots of their positive elements are contained in them (see [Neumann B.H.
1949] pp 211 ,4.91 Corollary).In other words
they are Pythagorean complete fields.
Theorem 8. (The Holder-type
classification theorem).
Every field
of ordinal characteristic á, denoted
by Fá (where á is a principal ordinal) is contained between the
fields Qá and Rá :QáÍFáÍRá .
Proof. Contained in the proofs of the theorem 7 and lemma 5 q.e.d.
Remark.9 The previous theorem gives that the hierarchy of ordinal real numbers
has universal embedding property for
the category of linearly ordered fields, that is every linearly ordered field
has an monomorphic image in some field of the hierarchy.The hierarchy of
transfinite real numbers is known to have, also, this property .Such
hierarchies we call universal
embedding hierarchies. Especially
the hierarchy of ordinal real numbers after the classification theorem 8
,we call also, universal classification hierarchy.
Remark.10 We notice that since every order type ë is order-embeddable in some transfinite real number
field R(ë) (see [Glayzal A. 1937] )as Archemidean base which in its turn is
embeddable in some ordinal real number field Rá ,the above two hierarchies as hierarhies of
order-types are universal embedding hierarchies for the category of
order-types .Let an order type ë ; the
least principal ordinal number á such that ë is order-embeddable (by a monomorphism) in the order-type and field Rá, is called the fundamental density of the
order type ë and is denoted by df(ë).
Remark. In the [ Massaza Carla, 1971] Definition I , is
defined which cuts are the Dedekind cuts in linearly
ordered fields .It is proved
also that the Dedekind
completion D(F) of a linaerly ordered field F is also its Cauchy completion (in the order topology ).If we
take the Dedekind completion D(Rá) of a field of ordinal real numbers Rá, it has
to be its Cauchy completion which
is again the Rá. Thus the fields of the ordinal real numbers are also
Dedekind complete . Conversely ,let any Dedekind complete linearly field
F .Let us denote with á its
ordinal characteristic .Then by the Holder type classification (theorem 8 ) it
is a subfield of the field Rá of ordinal real numbers of characteristic á .Since the Dedekind completion D(F) =F coincides with
the F and also with its Cauchy completion ,we get that F=Rá, because the Cauchy completion of F is the Rá. In other words the class of Dedekind complete fields
coincides with the class of the fields of
ordinal real numbers .
Summarising we mention that the fields of ordinal real
numbers have at least four kinds of completnesses that characterise them : Cauchy
completness ,Dedekind completness,completness up-to-characteristic,
Archemidean completness .It seems that he previous four
completnesses can be
summarised by saying
that there is
no cofinal (coterminal ) order field extensions of them ;in short they
are cofinally complete ,or cofinally maximal .They are also real
complete (closed ,Artin-Shreier ) and Pythagorean
complete.
Remark. By corollary 7 we get that the field Cá is the algebraic closure of Rá :Cá= 
.
We
close this paragraph by mentioning that an
axiomatic definition of the field Rá (á is a principal ordinal)
would be the following:
First
axiomatic definition of Rá.
The
field of ordinal real numbers Rá is the unique Funtamental
(Canchy)-complete, in the order-topology, field of characteristic á.
Second axiomatic definition of Rá .
The field
of ordinal real numbers Rá is the unique complete
(up-to-characteristic) field of
characteristic á .
These definitions apply even in the case
of the field of real numbers (a = ù).
§ 3 The arithmetisation of order-types .
Remark.As it is known the linear segments of elementary
Euclidean geometry can be defined as special order-types with Archimedean
property and Hilbert completness through axioms (see e.g. for a not ancient
approach the Hilbert axiomatisation in
[Hilbert D 1977] ch 1 ).Then ,they can be proved to be order isomorfic with
subsets of the real number field R. This is known as the elementary
arithmetisation of the order-types of Euclidean linear segments.
Proposition 10.(the K- funtamental
arithmetisation theorem of order-types.)
Every order-type ë is K-arithmetisable with ordinal numbers and has a
fundamental density df(ë) which is
a principal ordinal number .
In the next paper ,after the unification theorem of
the transfinite real ,surreal ,ordinal real numbers ,a second arithmetisation
theorem shall be proved. Two more universal hierarchies of formal power series
fields shall be, also, proved that they are universal embedding hierarchies .We
state these results here. For the definition of tree ,height of a tree, level of
a tree, binary tree e.t.c.see [Kuratowski K.-Mostowski A. 1968] ch ii § 1, § 2
. The binary tree of height the ordinal á we denote with Dá. After the
previously mentioned unification theorem 17 of the next paper we get
that the hierarchy
of binary trees
is a universal embedding hierarchy for the order- types . Since the
binary trees are subsets of linearly ordered fields and their elements
consisting exclusively from 1's in the binary sequence, correspond
to the ordinal
numbers with the Hessenberg
operations (see also [Conway J.H. 1976] ch 3 note pp 28 and also [ Kyritsis C. 1991Alt] the
characterisation theorem ) this universal
embedding property we call also
binary arithmetisation
.The least ordinal á such that
an order-type ë is order embeddable in the binary tree Dá ,we call the binary density of ë ,and we denote it by
db(ë).
Theorem 11
( The binary arithmetisation theorem of order-types )
Every order-type ë is binary arithmetisable and has
a binary density db(ë) which is
an ordinal number .
From the previous theorem ,by denoting a level of
height á of a binary tree ,by Tá ,and giving to the Cartesian product 
the lexicographical ordering ,we also get the
next :
Corollary 12. The formal power series hierarchies R((Dá)), 
, are universal embedding
hierarchies for the linearly ordered
fields .
§ 4 Some
general results on linearly ordered fields .
In this paragraph we give some results generally for
the category of linearly ordered fields. To save space we shall not give the
proofs, since they do not have serious dificulties,nevertheless we shall
indicate how they can be obtained .
Lemma 13 (On the rank and characteristic)
Let us suppose that the characteristic of
the field F is 
where á, is á limit
ordinal. It holds that the
rank of the extension F/K is a
cofinal order-type with the characteristic of the field F. That is cf(r(F/K))=
cf(charF)=cf(char F-char K).
Remark.For the definition of the rank of an extension
see [ Kyritsis C. 1991] § 4. For the proof of the previous theorem we use the
existence for any principal ordinal of the ordinal real numbers fields 
of characteristic .
Let F
be a linearly ordered field. If xF by L(x) we denote the set
L(x) = {y| yF y<x} and by R(x) the set
R(x) ={y| yF x<y}.
By
elementary arguments on linearly ordered
fields the following identities
can be proved.
Lemma
14
Let x,
y F. The following hold
1. L(-x) = - L(x) R(-x) = -R(x)
2. L(x+y) = L(x)+y = x+L(y)
R(x+y)
= R(x)+y = x+R(y)
3. L(x.y) = L(x).y + xL(y) - L(x).L(y) = R(x).y + xR(y) - R(x)R(y)
R(x.y)
= L(x).y+xR(y) - L(x).R(y) = R(x).y + xL(y) - R(x).L(y)
4. 
5. 
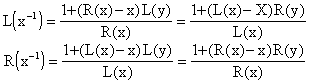
The
previous identities show also that the definition of operations used to define
the surreal number fields are not
something peculiar to
these fields but hold in any linearly ordered field
.
In the
next paper of this
work we will understand the true
peculiarity of the
technique of the surreal
numbers.
Lemma 15
If F/k is an extension of
two linearly ordered fields , it holds that
tr.d.(F/k) £ 2À(Char.F) where tr.d.is the transandental degree of the extension .
Remark. For the definition of the transandental
degree, base e.t.c see for instance [ Zariski O.-Samuel P. 1958] vol. I
pp. 95-102 also [Kyritsis C. 1991 ] § 4 ). The proof is obtained by using the
Holder-type classification for F :Qá Í F Í Rá where á=char(F).
The next proposition shows that all
the information of an extension of linearly ordered fields is to
be found in the ideal of infinitesimals (or in the infinite elements). Proposition 16. Let F/k, F'/k two
(ordered) extensions of the same linearly ordered field k. If the ideals
of K-infinitesimals of the extension denoted respectively by mF
and mF' are isomorphic as ordered integral domains ,then this
isomorphism is extendable to an algebraic
and order isomorphism of the fields F, F'.
Remark .The proof is direct from the definitions.
Remark. An extension F/k of the linearly ordered field k to
F, is transcendental if Char F>char k and then the field F is an infinite dimensional vector
space over k.
Proposition
17 .
Let F be
a linearly ordered
field of characteristic char(F)=
where á is a limit ordinal . It holds that the field F in the order topology is
totally disconnected .
Remark. The proof
uses the existence,
for every principal ordinal , of the fields of ordinal
real numbers R.
Theorem 18 The classes of
transfinite real numbers CR, and of ordinal real numbers Ù1R,
coinside.
Proof. Since both Hierarchies of transfinite real and
ordinal real numbers have the universal
embedding property (see remark 9 ) ,every transfinite real number-field is
contained in some ordinal real number-field and every ordinal real-number
field in some
transfinite real
number-field.Thus CR Í Ù1R and Ù1R Í CR, and CR = Ù1R . Q.E.D.
§ 5 The
A-Archimedeanity
The, at
least two different, definitions of
archemideanity, that can be found for instance in [Glayzal A. 1937] and in
other authors as in [ Conway J.H. 1976 ] or [ Arin E. Schreier O. 1927] give us
the opportunity to treat them in unified way through the concept of archemideanity
relative to a monoid.
The fact
that the linearly
ordered field F
has characteristic ù (the least infinite ordinal) is
equivalent with the statement that the field F is Archimedean according to any (classical) known
definition.
Let us denote by G a linearly ordered group
and by A a monoid of endomorphisms of
G as a group.
It is said
that x is A-Archimedean to y where x,yG iff there are a,bA with a(x)³y and b(y)³x. If A is the
domain Z of integers (the endomorphisms
are multiplication with
an integer )we simply say that x is Archimedean to y. If for
every pair x,y of elements of G holds that x is A-Archimedean to y, it is said
that G is A-Archimedean
Let F be a
linearly ordered field .If we consider it as an additive group, and we denote
by A1 a monoid of endomorphisms of the additive group , we get the concept of x being A-additively
Archimedean to y. If we consider the multiplicative group F* and
we take a monoid, denoted by A2, of edomorphisms of the
multiplicative group, we get the concept of x
being A-multiplicatively Archimedean to y.
Let A=A1VA2
be the monoid of mappings from F to F generated by the previous monoids . It is
said that x is A-field-Archimedean to y iff there are a, bA such that a(x)³y, b(y)³x.
In any
extension F/k of a field K by a field F, where F,k are fields of ordinal
characteristic with char
F>Char K, if we take as A1, to be the
multiplication with elements from the field K ( considering the field F as a linear space over K), we get the
concept of x being K-additively Archimedean to y.( For K=R this is also
known as "x is commensurate to y " see [Conway J.H. 1976] ch 3 pp 31
).
If A1
is the multiplication with integers and
A2 is power with integral exponents ,then it is simply
said that x is field Archimedean to y
(Known also from the A. Gleyzal’s
definition of Archimedeanity)
A
non-Archimedean linearly ordered field denoted by F is simply a linearly ordered field for which
not all pairs (x,y) of its elements are mutually additively Archimedean.
(Thus charF>ù ) But it can be very well
A-additively Archimedean for other monoids A.In particular if charF=á and A is the monoid of endomorphisms of the additive
group of F defined by (field )
multiplication with ordinals less than á, then it is A-additively Archimedean
and we denote it by writing that it is á-additively Archimedean
Acknowledgments. I would like to thank professors W.A.J.Luxemburg and
A. Kechris (Mathematics Department of the CALTECH) for the interest they showed
and that they gave to me the opportunity to lecture about the ordinal real
numbers in CALTECH. Also the professors H. Enderton and G.Moschovakis
(Mathematics Department of the UCLA) for their interest and encouragement to
continue this project.
Bibliography
[N. L. Alling 1987] Foundations of analysis over surreal number fields
North-Holland Math.Studies V. 141 1987 .
[Artin E.
Schreier O.1927] Algebraishe konstruktion reellerkorper,Abh. Math. Sem.Univ. Hamburg 5 (1927) pp
85-99 .
[Artin E. - Tate J. 1967] Class Field
Theory Benjamin 1967.
[Baer Reinold 1970 ] Dichte,Archimedizitat und Starrheit geordneter Korper,
Mathematische Annalen 188 pp 165-205,1970.
[Baker Alan 1975] Trancendental Number Theory Cambridge University Press,
1975.
[Bourbaki N1952] Elemente de Mathematique algebre, chapitre III Hermann Paris 1948, chapitre VI
Hermann Paris 1952.
[Brown Ron 1971 ] Real places and Ordered Fields Rocky Mountain Journal of
Mathematics, Vol 1 ,pp 633-636, 1971.
[Brown R.,Craven T.C., Ordered fields satisfying
Rolle's Theorem
Pelling M.J.1986] Illinois Journal of Mathematics Vol
30, n 1 Spring 1986 pp 66-78.
[Clliford A. H,1954] Note on
Hahn's theorem on ordered
abelian groups. Proc. of the Amer. Math. Soc. 5 (1954) pp 860-863.
[Cohen L.W.-
Goffman C,1949] Theory
of transfinite
Convergence.Transact. of the Amer. Math. Soc. 66 (1949) pp 65-74.
[Cohn P.M,1965] Universal Algebva
Harper - Row 1965 .
[Conway J.H,1976] On
numbers and games Academic press 1976 .
[Cuesta Dutardi
N,1954] Algebra
Ordinal Rev. Acad. Cientis Madrid 4 (1954) pp 103-145 .
[Dugundji J,1966] Topology, Allyn and
Bacon inc. 1966.
[Ehreshmann Ch,1956] Categories
et structure Dunod 1956
[Ehrlich P,1988] An alternative construction of Conway's Ordered
Field No, Algebra Universalis 25 (1988)
pp 7-16 .
[Ehrlich P] The Dedekind completion of No ,submitted to
Algebra Universalis.
[Endler O,1972] Valuation
Theory, Springer 1972.
[Erdos P.-Gillman L.- An
isomorphism theorem for real closed fields
Henrkiksen
M,1955] Ann. of
Math.(2) 61 (1955)pp 542-554.
[Frankel A.A,1953] Abstract set Theory.
North - Holland 1953.
[Fuchs L,1963] Partially ordered algebraic systems Pergamon Oxford 1963.
[Gillman L.-Jerison
M,1960] Rings of continuous functions. Van Nostrand Princeton 1960.
[Gleyzal A,1937] Transfinite real numbers. Proc. of the Nat. Acad.of
scien. 23 (1937) pp 581-587.
[Gravett K.A.H,1956] Ordered
abelian groups. Quart. J. Math. Oxford 7 (1956) pp 57-63.
[Hahn H,1907] Uber
die nichtarhimedishen Grossensysteme.S.
Ber. Akad. Wiss. Wein. Math. Natur.Wkl Abt. IIa
116 (1907) pp 601-655.
[Hausner M.-Wendel
J.G,1952] Ordered Vector Spases Proc. of the Amer. Math. Soc.3 (1952) pp
977-982.
[Hessenberg G,1906] Grundbegriffe der Mengenlehre (Abh. der Friesschen Schule, N.S. [1] Heft 4) Gottingen 220 1906).
[Hilbert D,1977] Grundlagen der Geometry Teubner Studienbucher 1977 .
[Hilbert D. -Ackermann W.,1950] Principles
of Mathematical Logic. Chelsea Pub.
Comp. N.Y. 1950.
[Kaplansky I,1942] Maximal fields with valuations Duke Math. J. 9
(1942) pp 303-321.
[ Krull W,1931] Allgemeine Bewertungs theorie. J.reine angew. Math.
176 (1931) pp 160-196.
[Kuratowski K,1966] Topology v.I v.II
Academic Press 1966.
[Kuratowski K. -Mostowski
A,1968] Set Theory
North - Holland 1968.
[ Kyritsis
C.E1991] Algebraic characterisation of the
Hessenberg operations in the ordinal numbers. (unpublished yet).
[Kyritsis C.E1991] Ordinal real numbers 1. The ordinal characteristic.
[Lang S,1984] Algebra .
Addison-Wesley P.C. 1984 .
[Lam T.Y,1980] The
Theory of Ordered Fields Ring theory and Algebra III. Edited by
B.R. McDonald Dekker 1980 pp
1-268.
[Laugwitz Detler ,1983 ] V
Calculus as a Generalization of Field Extension. An alternative approach
to non-Standard analysis "Recent developments in
non-standard analysis" Lecture Notes in Math 983 Springer 1983.
[MacLane S,1939] The
Universality of Formal Power Series fields.Bull. of the Amer.
Math. Soc. 45 (1939) pp 880-890.
[MacLane S,1971] Categories for the working mathematician Springer 1971
[Massaza ,Carla,1971 ] On the comletion of ordered fields. Practica (=Proceedings)
of the Academy of Athens ,Vol 45 ,1970 (published 1971 )
[Monna A.F,1970] Analyse non-Archimedienne Springer 1970.
[Munkress J.R,1975] Topology. Prenctice Hall 1975.
[Nachbin L,1976] Topology
and Order. Robert E.Krieger P.C.
N.Y. 1976.
[Neubrunnova Anna,1980 ]
On transfinite convergence and generalised continuity.
Mathematica Slovaca vol 30,1, 1980.
[Neumann B.H.,1949] On ordered division rings. Transact. of the Amer. Math. Soc.
66 (1949) pp 202-252. .
[Prestel Alexander,1980 ] Lectures
on formaly real fields .Lecture Notes 1093, Springer ,1980 .
[Robinson A,1966] Non-Standard analysis.
North - Holland 1974 (1966).
[Robinson A.,1972 ] On thr real Closure of a Hardy Field. pp 427-433 in the Theory of Sets and
topology. A Collection of papers
in honour of
Felix Hausdorff , VEB ,1972 .
[Rolland,Raymond . 1981 ]
Etudes des courpure dans
les groupes et corps ordonnes. Dans Geometrie Algebrique Reeles et Formes
Quadradiques. Rennes 1981. Proceedings, Lecture Notes in Mathematics 959
Springer ,pp 386-405 .
[Rudin W,1960] Fourier analysis on groups. Interscience Pub 1960 .
[Shilling O.F.G,1972] The
theory of valuastions. Amer. Math. Soc. 1950.
[Schubert H,1972] Categories Springer 1972.
[Scott, Dana , 1969] On
Completing Ordered Fields. In Applications of Model theory to Algebra, Analysis
and Probability edited by W.A.J. Luxenburg pp 274-278, Holt Rinehart and
Winston 1969.
[Sirkoski R,1948] On an ordered algebraic field. Warsow, Towarzytwo
Nankowe Warzawskie 41 (1948) pp 69-96.
[Stone A.L,1969] Non-Standard analysis in
topological algebra in Applications of
Model Theory to
Algebra, Analysis and
Probability N.Y. (1969) PP
285-300.
[Stroyan, K.D. and Introduction
to the theory of Infinitecimals
Luxenburg W.A.J,1976] N.Y.1976.
[Lynn A.Steen- Counterexamples in
Toplogy Springer 1970 .
Seebach J.A. Jr,]
[Viswanathan T.M,1977] Ordered
fields and sign-changing polynomials. Journal fur reine und angewante
Mathematik, 296 pp 1-9,1977.
[Van der Waerden
B.L,1970] Algebra V1
V2 Frederick Unger Pub. Co. N.Y.
1970.
[Weil A,1967] Basic Number
Theory, Springer Verlag Berlin,
Heidelberg N.Y. 1967.
[Zakon E,1955] Fractions
of ordinal numbers Israel
Institute of Tecnology Scient. Public. 6, 94-103 1955.
[Zariski O. -Samuel
P,1958] Commutative
Algebra V.I.II Springer 1958.
[Zervos,S.P.1961] Sur les rapportes
entre la completions la cloture algebrique des corps commutatifs de
caracteristique zero C.R. Acad. Sc. Paris, 5 Avril 1961 t. 282 pp 2053-2055.
[Zervos,S.P.1991] Simple
abstract and concrete
considerations suggested by Thue's theorem. Mathematics revisited,
mathematicians remembered Vol.1 1991.pp
1-68.
List of
special symbols
á,â,ù
: Small Greek letters
Ù1 :
Capital Greek letter
omega with the subscript 1
Fa :
Capital letter F with
superscript a.
N
: Capital Aleph ,the first letter
of the hebrew alphabet . In the text is used a capital script. letter n .
: cross in a circle, point in a circle .
Ná,Zá,Qá,Rá,: Roman capital
letters with subscript small
Greek letters
Cá,Há
*×, *R et.c
: Capital standard or roman
letters with left superscript a star.
CN,CZ,CQ, :Capital standard
letter c followed
by capital letters
C*R, with possibly
a left superscript a star
:
Capital tstandard letter with a cap.
Ó
: Capital Greek letter sigma
:
Capital standard D with subscript
a small Greek letter and in upper place a small zero.
Ordinal real numbers 2.The arithmetisation of order types .
by
Dr.Konstantin E.Kyritsis
Mathematics Dept.
University of the Aegean
Karlovassi 83200
Samos Greece
Abstract
In this
paper the main results are :Proofs that the ordinal real numbers are real
closed fields and complete up-to-characteristic .They are also Dedekind ,and
Archemidean complete fields .They are real formal power series fields and
Pythagorean complete fields It is proved
and discussed the K-fundamental
arithmetisationand the binary
arithmetisation of the order
types .
Subject Classification of AMS 03,04,08,13,46
Key
words
real closed commutative fields
Grothendick group
Archemidean complete fields
linearly ordered commutative fields
full binary
trees